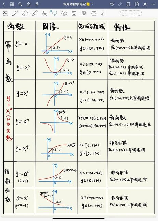
在我们高中的数学教科书中,经常会遇到关于抛物线准线方程的推导题,对于那些以复杂的解法进行推导的同学们,或许可以试着换一种简单的方式来解决这类问题。
首先,我们回忆一下抛物线的的正式方程式:$y=ax^2 bx c$,然后我们将它化归为对称轴平移的标准方程:$y=a(x-h)^2 k$。
接下来,我们将问题转化为抛物线上任意一点的切线方程,通过求出所有的切线方程来确定抛物线的准线方程。
以切点为$(x_0,y_0)$的切线方程为$y=a(x_0-h)(x-x_0) (y_0-k)$,然后,我们通过求导的方式得到该点切线斜率为$a(x_0-h)$,其中$x_0,y_0$代入标准方程可得出$k=b/(4a)$,和$h=-b/(2a)$,带回切线公式中可得出每个切线方程,由此我们可以得出抛物线的准线方程。
通过这样的方式,可以简单的推导出抛物线的准线方程,这个方法不仅速度快,也方便我们对于题目的理解和掌握。